Learned Filters

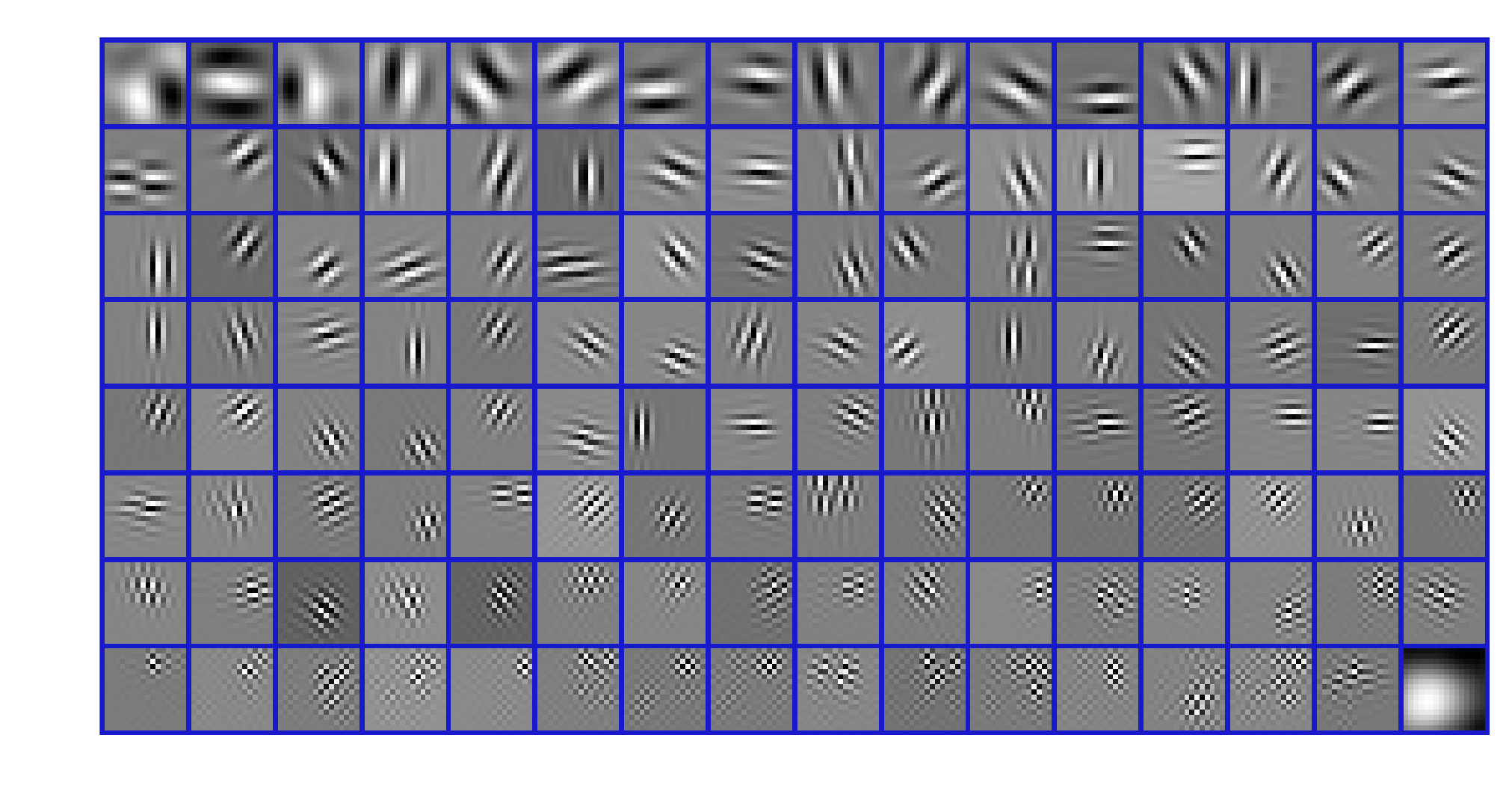
These are examples of 16x16 sparsifying filters, as described in [1]. They were learned on a set of five images and are constrained to form a frame for the space of N by N images. While the filters appear similar to Gabor atoms or the filters learned with a convolutional neural network, they were learned to satisfy a significantly different optimality condition.

1. L. Pfister and Y. Bresler, “Learning Filter Bank Sparsifying Transforms,” IEEE Transactions on Signal Processing, vol. 67, no. 2, 2019.
   • Abstract
   Data is said to follow the transform (or analysis) sparsity model if it becomes sparse when acted on by a linear operator called a sparsifying transform. Several algorithms have been designed to learn such a transform directly from data, and data-adaptive sparsifying transforms have demonstrated excellent performance in signal restoration tasks. Sparsifying transforms are typically learned using small sub-regions of data called patches, but these algorithms often ignore redundant information shared between neighboring patches. We show that many existing transform and analysis sparse representations can be viewed as filter banks, thus linking the local properties of patch-based model to the global properties of a convolutional model. We propose a new transform learning framework where the sparsifying transform is an undecimated perfect reconstruction filter bank. Unlike previous transform learning algorithms, the filter length can be chosen independently of the number of filter bank channels. Numerical results indicate filter bank sparsifying transforms outperform existing patch-based transform learning for image denoising while benefiting from additional flexibility in the design process.
   • Download
   • Link to Publisher
   • BibTeX

   @article{Pfister2018-Learn-Filter,
     author = {Pfister, Luke and Bresler, Yoram},
     title = {Learning Filter Bank Sparsifying Transforms},
     journal = {IEEE Transactions on Signal Processing},
     volume = {67},
     number = {2},
     pages = {504-519},
     year = {2019},
     doi = {10.1109/tsp.2018.2883021},
     url = {https://doi.org/10.1109/tsp.2018.2883021}
   }